Перейти к:
Моделирование конкурентных взаимодействий: базовые закономерности. Часть 1
https://doi.org/10.21202/2782-2923.2023.1.35-50
EDN: LUERWY
Аннотация
Цель: анализ общих закономерностей социально-экономической и политической динамики (как внутри общества, так и в межгосударственных отношениях), обусловленных наличием конкуренции между ключевыми экономическими и политическими акторами.
Методы: для исследования конкурентных взаимодействий используются методы математического динамического моделирования.
Результаты: отношение к конкуренции как социальному явлению является неоднозначным. Она рассматривается то как положительный (например, в исследованиях по рыночной экономике), то как отрицательный (например, при рассмотрении межгосударственных конфликтов) фактор. В работе предпринята попытка проанализировать общие особенности конкурентных взаимодействий на основе исследования базовой математической модели, описывающей конкуренцию в социально-экономической и социально-политической сферах. С использованием базовой математической модели рассмотрены различные режимы конкурентных взаимодействий, определены условия перехода от одних режимов к другим, приведены примеры реализации этих режимов в экономике.
Научная новизна: в ходе исследования с использованием математического моделирования основное внимание уделено так называемым негрубым (по А. А. Андронову) случаям реализации конкурентного взаимодействия, которые до сих пор редко рассматривались в научной литературе, но зато часто встречаются в реальной жизни.
Практическая значимость: результаты анализа и математического моделирования позволяют установить, при каких условиях стимулирование конкуренции способствует экономическому развитию, а при каких приводит к кризисным ситуациям.
Ключевые слова
Для цитирования:
Малков С.Ю. Моделирование конкурентных взаимодействий: базовые закономерности. Часть 1. Russian Journal of Economics and Law. 2023;17(1):35-50. https://doi.org/10.21202/2782-2923.2023.1.35-50. EDN: LUERWY
For citation:
Malkov S.Yu. Modeling of competitive interactions: basic regularities. Part 1. Russian Journal of Economics and Law. 2023;17(1):35-50. (In Russ.) https://doi.org/10.21202/2782-2923.2023.1.35-50. EDN: LUERWY
Введение
Конкурентные отношения характерны для социальных взаимодействий на протяжении всей человеческой истории, они во многом определяют специфику экономических и политических процессов как на межгосударственном уровне, так и во внутренней жизни каждой страны. При этом отношение к конкуренции как явлению весьма неоднозначное: в научных исследованиях она рассматривается то как фактор, стимулирующий экономическую и политическую активность, способствующий динамичному развитию общества, то как фактор, препятствующий решению важных для государства политических и экономических задач, мешающий консолидации усилий общества по преодолению имеющихся проблем.
В этой связи представляет интерес проведение анализа закономерностей конкурентных взаимодействий на теоретическим уровне. Целесообразно посмотреть на конкурентные взаимодействия не в контексте какой-то конкретной ситуации, а как на объект математического моделирования, позволяющего охватить многообразие частных ситуаций. В данной статье будет реализован именно этот подход. На основе математической модели общего вида будут рассмотрены основные режимы конкурентных отношений в социальных системах и условия перехода от одного режима к другому. Также будет рассмотрено несколько сюжетов, иллюстрирующих использование математического моделирования для лучшего понимания внутренней логики процессов, происходящих в обществе.
Базовая математическая модель конкурентных взаимодействий и ее особенности
Моделированию конкурентных взаимодействий в политике, экономике, военной сфере посвящено большое количество работ (см., например, обзоры [1][2]). Нас будут интересовать наиболее общие закономерности, поэтому мы, следуя работе [3. С. 506–507], будем рассматривать базовую модель конкурентной борьбы, которая может быть представлена системой дифференциальных уравнений, описывающих изменение соотношения сил различных акторов (от английского act – «действовать») в ходе конкурентных взаимодействий:
dui / dt = Ai (ui) – Bi (ui) + ∑j = i Cij (ui, uj), i, j = 1, 2, 3, …, N. (1)
Здесь t – время; N – количество взаимодействующих акторов; ui – показатель, характеризующий «силу» (степень влияния, доминирования, экономической мощи и т. п.) i-го актора в момент времени t. Член Ai (ui) описывает воспроизводство (возобновление) «силы» i-го актора. Член Bi (ui) описывает снижение «силы» i-го актора вследствие процессов, непосредственно не связанных с конкурентной борьбой (отрицательные обратные связи в социальной системе, ресурсные ограничения и т. п.). Члены Cij (ui, uj) описывают взаимодействие между акторами. В случае когда это взаимодействие конкурентное, данные члены отрицательны, поскольку в конкурентной борьбе акторы стремятся подавить (ослабить) друг друга.
В упрощенном виде (при сохранении только линейных и квадратичных членов в правых частях уравнений (1)), базовая модель конкуренции может быть записана следующим образом:
dui / dt = ai · ui – bi · ui2 + ∑j = i cij · ui · uj; i, j = 1, 2, 3, …, N; ai > 0, bi > 0. (2)
Динамика системы (2) при постоянных значениях коэффициентов ai, bi, cij рассматривалась во многих работах1. В статье [7] подробно рассмотрены особенности динамики системы (2) в случае взаимодействия двух акторов (N = 2) при разных соотношениях значений коэффициентов с иллюстрацией этой динамики на фазовых портретах. Фазовые портреты – это графики в пространстве переменных ui, отражающие совокупность траекторий этих переменных, задаваемых рассматриваемой системой уравнений. Форма этих траекторий при разном соотношении коэффициентов будет разная. На рис. 1 и 2 приведены фазовые портреты для наиболее интересных для нас случаев2 для взаимодействия двух акторов (сплошными линиями на рисунках обозначены изоклины, на которых траектории изменяют направление движения; кружочками обозначены устойчивые аттракторы – состояния, к которым эволюционирует система с течением времени):
du1 / dt = a1 · u1 – b1 · u12 + c12 · u1 · u2, (3)
du2 / dt = a2 · u2 – b2 · u22 + c21 · u1 · u2. (4)
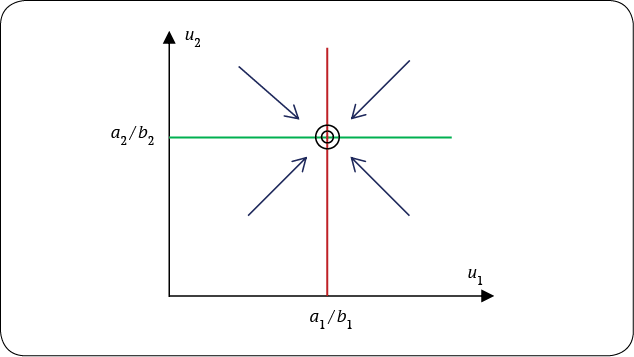
Рис. 1. Фазовый портрет системы (3) – (4) с типовыми траекториями при отсутствии взаимодействия между акторами (cij = 0)
Источник: составлено автором.
Fig. 1. Phase portrait of the system (3) – (4) with typical trajectories in the absence of interaction between actors (cij = 0)
Source: сompiled by the author.
Рисунок 1 отражает ситуацию, когда взаимодействие между акторами отсутствует (автономное развитие акторов при cij = 0). Эта ситуация является отправной точкой для нашего анализа. Ее характерной чертой является наличие состояния устойчивого равновесия (аттрактор с координатами u1 = a1 / b1, u2 = a2 / b2), к которому стремится система вне зависимости от того, в каком начальном состоянии она находится.
Рисунки 2А – 2Г отражают ситуацию, когда акторы взаимодействуют друг с другом и при этом величины cij изменяются от больших положительных значений к большим отрицательным (при этом для наглядности изображения фазовых портретов все остальные коэффициенты приняты равными единице: ai = bi = 1).
Рисунок 2А отражает ситуацию, когда cij > 0 и c1 · c2 > b1 · b2. Для нее характерен непрерывный рост как u1, так и u2. Взаимодействие приводит к улучшению состояния обоих акторов.
Рисунок 2Б отражает ситуацию, когда cij > 0, но c1 · c2 < b1 · b2. Для нее характерно наличие устойчивого аттрактора с координатами u1 > a1/b1, u2 > a2 / b2. Взаимодействие приводит к улучшению состояния обоих акторов.
Рисунок 2В отражает ситуацию, когда cij < 0 и |c1| · |c2| < b1 · b2. Для нее характерно наличие устойчивого аттрактора с координатами u1 < a1 / b1, u2 < a2 / b2. Взаимодействие приводит к ухудшению состояния обоих акторов.
Рисунок 2Г отражает ситуацию, когда cij < 0 и |c1| · |c2| > b1· b2. Для нее характерно наличие устойчивого аттрактора с координатами u1 < a1 / b1, u2 < a2 / b2. Взаимодействие приводит к полному подавлению одного актора другим. При этом существенным является начальное состояние системы. Вся фазовая плоскость делится на две зоны, разделяемые сепаратрисой (обозначена на рисунке штрихпунктирной линией): если изначально акторы находятся в зоне 1, то в конечном итоге побеждает первый актор, если же изначально акторы находятся в зоне 2, то побеждает второй актор.
Рисунки 2А – 2Г характеризуют ситуации, когда система (3) – (4) является «грубой» по А. А. Андронову [9], т. е. когда ее изоклины пересекаются. Однако не исключены ситуации, когда изоклины либо параллельны, либо сливаются в одну прямую (тогда точек равновесия становится бесконечно много). Такое возможно при выполнении условия cij < 0 и |c1| · |c2| = b1 · b2. Любопытно, что именно этот случай и близкие к нему наиболее интересны при анализе конкуренции в социальных системах, поэтому ниже мы рассмотрим такие ситуации более детально на примере нескольких сюжетов.
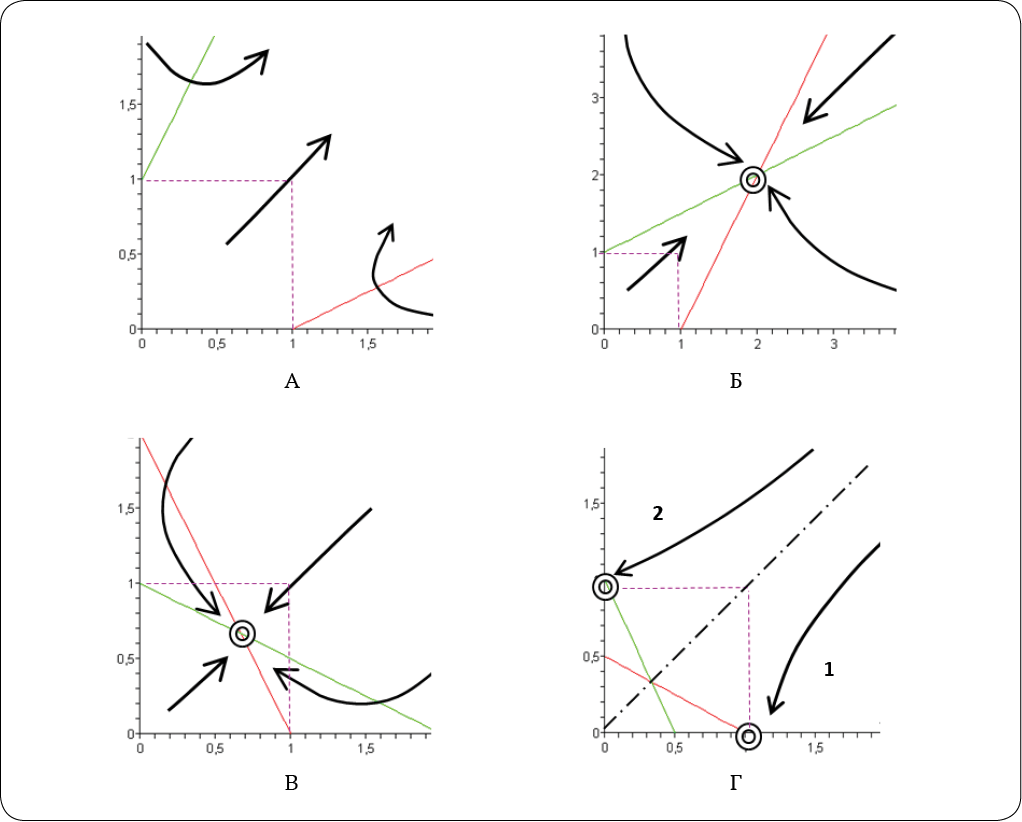
Рис. 2. Фазовые портреты с типовыми траекториями при наличии взаимодействия между акторами (cij ≠ 0)
для различных соотношений значений коэффициентов в модели (3) – (4)
Примечание: по оси абсцисс отложены значения u1, по оси ординат – значения u2.
Источник: составлено автором.
Fig. 2. Phase portraits with typical trajectories in the presence of interaction between actors (cij ≠ 0)
for different ratios of coefficient values in the model (3) – (4)
Note: the u1 values are shown along the abscissa axis, and the u2 values are shown along the ordinate axis.
Source: сompiled by the author.
Экономическая конкуренция и ее особенности
- Принято считать, что в экономике конкуренция – это положительный фактор, способствующий экономическому росту. С другой стороны, считается, что жесткая (так называемая недобросовестная) конкуренция приводит к монополизму, который вреден для экономического развития. Неизбежно возникают вопросы: Как в конкретной ситуации определить, добро или зло несет конкуренция? Есть ли четкие критерии, когда конкуренция полезна, а когда вредна? Попробуем ответить на эти вопросы, по крайней мере, на качественном уровне, используя базовую модель.
При первом взгляде на рис. 2А – 2Г приходит мысль, что конкуренция, соответствующая отрицательным значениям коэффициентов cij, это в любом случае негативный фактор, поскольку приводит либо к общему ухудшению ситуации и перемещению состояния равновесия в область низких значений (рис. 2В), либо к полному подавлению одного из акторов (рис. 2Г).
Однако не все так прямолинейно. Рассмотрим феномен экономической конкуренции более подробно применительно к различным историческим эпохам. Смысл экономической конкуренции заключается в том, что несколько экономических акторов работают в одной экономической нише, предлагая потенциальным покупателям сходную по своим потребительским свойствам продукцию, тем самым конкурируя за потребительский спрос, который ограничен. Для случая, когда конкурируют N экономических акторов, модель экономической конкуренции в обобщенном виде может быть представлена следующим образом:
dMi / dt = (выручка от продажи продукции) – (производственные, транспортные и другие расходы, связанные с экономической деятельностью) = ki · MH – fi (Fi), (5)
где Mi – денежные средства i-го экономического актора; MH – общий объем потребительского спроса на предлагаемую акторами продукцию, выраженный в деньгах; ki – доля общего потребительского спроса, которая достается i-му экономическому актору в единицу времени от продажи его продукции; Fi – объем продукции, предлагаемый к продаже i-м экономическим актором; fi (Fi) – расходы i-го актора, зависящие от объема проданной им продукции. Конкретные значения ki, MH, Fi, а также вид функции fi (Fi) определяются особенностями рассматриваемой ситуации и в общем случае зависят как от внешних условий, так и от действий самих экономических акторов.
1.1. Рассмотрим, к каким выводам приводит модель (5) применительно к доиндустриальной (аграрной) эпохе. В аграрном обществе доминировало натуральное хозяйство, конкурентные рыночные отношения и борьба за рынки имели место по существу лишь в сегменте международной торговли. При этом торговля шла в основном элитными товарами (товарами престижа), поскольку только элита обладала значительными денежными средствами и могла обеспечить денежный спрос на заморские товары. Примером торговой конкуренции в Средние века является соперничество Генуэзской и Венецианской республик.
Применительно к случаю конкуренции двух (i = 1, 2) соперничающих торговых корпораций в некотором регионе (государстве) уравнения базовой модели (5) могут быть записаны в виде:
dM1 / dt = k1 · MH – h1 · F1, (6)
dM2 / dt = k2 · MH – h2 · F2, (7)
где Mi – денежные средства i-й торговой корпорации; MH – общий объем потребительского спроса в рассматриваемом регионе; ki – доля общего потребительского спроса, которая достается i-й торговой корпорации в единицу времени от продажи ее товаров в рассматриваемом регионе; Fi – объем товаров, продаваемых i-й торговой корпорацией; hi – коэффициент пропорциональности (считается, что расходы i-го актора пропорциональны объему торгового оборота).
Поскольку выручка от продаж пропорциональна объемам проданных товаров, то в предположении, что потребительские свойства товаров обеих корпораций одинаковы, из (6) – (7) получаем:
dM1 / dt = k'1 · (F1 / (F1 + F2)) · MH – h1 · F1, (8)
dM2 / dt = k'2 · (F2 / (F1 + F2)) · MH – h2 · F2, (9)
где k'1 и k'2 – коэффициенты, отражающие влияние внеэкономических факторов на величину выручки (например, влияние таможенных и иных сборов и налогов, избирательно устанавливаемых местными властями).
Пусть в экономическом плане удельные (на единицу товара) издержки обеих корпораций одинаковы (h1 = h2), а количество предлагаемого товара Fi пропорционально Mi (т. е. объемы торговли пропорциональны финансовой мощи корпораций: Fi ~ Mi), тогда имеем hi · Fi = h' · Мi и формулы (8) – (9) преобразуются следующим образом:
dM1 / dt = k'1 · (М1 / (М1 + М2)) · MH – h' · М1, (10)
dM2 / dt = k'2 · (М2 / (М1 + М2)) · MH – h' · М2. (11)
Система (10) – (11) не имеет устойчивого состояния равновесия. Выражения для изоклин системы (10) – (11) равны3:
M2 = (k'1 / h') · MH – M1, (12)
M2 = (k'2 / h') · MH – M1. (13)
Видно, что при k'1 = k'2 изоклины совпадают, а при k'1 ≠ k'2 представляют собой параллельные прямые (т. е. реализуется «негрубый», по А. А. Андронову, случай). Фазовый портрет системы (10) – (11) при k'1 > k'2 изображен на рис. 3.

Рис. 3. Фазовый портрет системы (10) – (12) при условии k'1 > k'2 .
Примечание: жирной точкой отмечено состояние устойчивого равновесия (оно соответствует экономическому поражению второй торговой корпорации в конкурентной борьбе с первой). В зоне I значения M1 и M2 растут, в зоне II значения M1 и M2 уменьшаются, в зоне III значение M1 растет, а значение M2 уменьшается.
Источник: составлено автором.
Fig. 3. Phase portrait of the system (10) – (12) at k'1 > k'2 .
Note: the bold point indicates a state of stable equilibrium (it corresponds to the economic defeat of the second trading corporation in competition with the first one). In zone I the values of M1 and M2 increase, in zone II the values of M1 and M2 decrease, in zone III the value of M1 increases, and the value of M2 decreases.
Source: сompiled by the author.
Из фазового портрета видно, что конкурентная борьба приводит к полному вытеснению одного из конкурентов из рассматриваемого региона, причем решающую роль при прочих равных условиях играют внеэкономические факторы получения преимуществ (подкуп, рейдерские захваты, силовые методы и т. п.). Действительно, в эпоху аграрного общества торговая конкуренция часто носила силовой характер (примером являются неоднократные войны в XIII–XV вв. между Генуэзской и Венецианской торговыми республиками) и, по существу, сводилась к разграничению зон влияния, внутри которых устанавливался монополизм одной из сторон.
1.2. Рассмотрим, к каким выводам приводит модель (5) применительно к индустриальной эпохе. В эту эпоху доминирует рыночная экономика с развитым денежным обращением. Производители конкурируют за потребительский спрос, поставляя продукцию на рынок, где в результате взаимодействия спроса и предложения устанавливаются цены на данную продукцию4.
На микроэкономическом уровне конкуренция между различными фирмами рассматривается во многих работах, в том числе с использованием математического моделирования. Однако в этих работах цены, как правило, задаются экзогенным образом, поскольку считается, что в отсутствие монополизма отдельные фирмы не могут влиять на уровень цен, формирующихся на свободном рынке. Математическое моделирование для анализа конкурентных отношений на мезоэкономическом уровне используется значительно реже (см., например, [10–12]), но именно этот уровень наиболее интересен, поскольку на нем возникает возможность в явном виде записать уравнения для ценообразования. Интересующая нас ситуация рассматривалась в работе [13]. Ниже приведены полученные в этой работе результаты, важные для нашего изложения5.
В работе [13. С. 45–49] рассматривалась замкнутая6 экономическая система, состоящая из двух подсистем, производящих однотипные товары, и двух групп домашних хозяйств, которые работают в этих подсистемах, получают зарплату и покупают на заработанные деньги продукцию, производимую подсистемами. Поскольку товары однотипные, то домашние хозяйства могут покупать продукцию как одной, так и другой подсистемы в соответствии со своими предпочтениями, при этом платежеспособный спрос домашних хозяйств ограничен их зарплатами. Модель описывает динамику денежных средств данных экономических акторов: MY1 – денежные средства первой подсистемы, MY2 – денежные средства второй подсистемы, MH1 – денежные средства первой группы домашних хозяйств, MH2 – денежные средства второй группы домашних хозяйств.
В качестве отправной точки анализа рассматривается ситуация, когда подсистемы производят идентичную продукцию, пользующуюся одинаковым потребительским спросом. В этом случае базовая модель (5), на мезоэкономическом уровне описывающая динамику денежных средств, может быть записана следующим образом:
dMY1 / dt = (k1 · MH1 + k2 · MH2) · (F1 / (F1 + F2)) – p · h1 · F1. (14)
dMH1 / dt = p · h1 · F1 – k1 · MH1. (15)
dMY2 / dt = (k1 · MH1 + k2 · MH2) · (F2 / (F1 + F2)) – p · h2 · F2. (16)
dMH2 / dt = p · h2 · F2 – k2 · MH2. (17)
dp / dt = a · ((k1 · MH1 + k2 · MH2) / (F1 + F2 – kY1 · MY1 / p – kY2 · MY2 / p) – р). (18)
Fi = fi · (kYi · MYi/p)ci. (19)
MH1 + MH2 + MY1 + MY2 = M. (20)
Уравнения (14) и (16) описывают динамику денежных средств, соответственно, первой и второй производственных подсистем. Правые части уравнений отражают баланс доходов и расходов в рассматриваемый момент времени. Считается, что доходы – это деньги, которые получают подсистемы, продавая домохозяйствам произведенные товары (считается, что поток этих денег пропорционален количеству произведенной подсистемой потребительской продукции Fi и общим денежным средствам домашних хозяйств; k1 и k2 – коэффициенты пропорциональности). Расходы подсистем – это выплачиваемые своей группе домашних хозяйств зарплаты за работу по производству продукции (считается, что зарплата носит сдельный характер, соответственно, она пропорциональна количеству производимой продукции и индексируется с учетом фактической инфляции; h1 и h2 – коэффициенты пропорциональности; p – уровень цен).
Уравнения (15) и (17) описывают динамику денежных средств, соответственно, первой и второй групп домашних хозяйств. Правые части уравнений отражают баланс доходов и расходов в рассматриваемый момент времени. Считается, что доходы – это зарплаты, получаемые от подсистем, а расходы – это деньги, расходуемые на покупку произведенных подсистемами потребительских товаров. Доходы подсистем являются расходами домашних хозяйств, а расходы подсистем являются доходами домашних хозяйств.
Уравнение (18) описывает динамику уровня цен. Считается, что он изменяется в зависимости от баланса денежного спроса на потребительскую продукцию и количественного предложения этой продукции. Количество потребительской продукции определяется как вся произведенная продукция минус продукция производственного назначения (необходимая для обеспечения производственного процесса).
Уравнение (19) – это производственная функция. Считается, что общее количество произведенной подсистемами продукции пропорционально их денежным инвестициям в производственный капитал (равным соответственно kY1 · MY1 и kY2 · MY2) с учетом инфляции и эффекта убывающей отдачи (с1 и с2 – коэффициенты убывающей отдачи).
Уравнение (20) отражает замкнутость экономической системы (М – общее количество денег в системе) и является по существу законом сохранения денег.
Для упрощения анализа будем считать, что скорость установления цены существенно выше скорости изменения Mi (что, как правило, хорошо выполняется в эффективно функционирующих рыночных экономиках). Тогда по теореме А. Н. Тихонова (1952) уравнение (18) может быть записано в виде:
k1 · MH1 / p + k2 · MH2 / p – (F1 + F2 – kY1 · MY1 / p – kY2 · MY2 / p) ≈ 0. (21)
Примем для упрощения анализа, что ki = k. Тогда из (21) и (20) следует:
p ≈ k · M / (F1 + F2 ). (22)
Соответственно, из (14), (16) и (22) следует:
dMY1 / dt ≈ k · (M – MY1 – MY2) · (F1 / (F1 + F2)) – k · M · h1 · F1) · (F1 / (F1 + F2)) = k · (M · (1 – h1) – MY1 – MY2) · (F1 / (F1 + F2)). (23)
dMY2 / dt ≈ k · (M – MY1 – MY2) · (F2 / (F1 + F2)) – k · M · h2 · (F2 / (F1 + F2)) = k · (M · (1 – h2) – MY1 – MY2) · (F2 / (F1 + F2)). (24)
Рассмотрим ситуацию, когда количество денег в экономической системе неизменно, т. е. денежная эмиссия отсутствует. Это означает, что выполняется условие:
M (t) = const. (25)
Данную ситуацию в соответствии с терминологией теории игр можно охарактеризовать как «игру с нулевой суммой» (ИсНС), при которой если у кого-то ресурс увеличился (в данном случае денежный ресурс), значит, у кого-то другого он уменьшился при сохранении общего количества ресурса в системе.
Для построения фазового портрета системы (23) – (24) необходимо определить выражения для изоклин (рис. 4). Их можно получить, если приравнять нулю правые части уравнений (23) и (24). В результате получаем:
M · (1 – h1) – MY1 – MY2 = 0, (26)
M · (1 – h2) – MY1 – MY2 = 0. (27)
Если удельные издержки (себестоимость продукции) у обеих подсистем одинаковые, т. е. hi = h, то фазовый портрет имеет следующий вид (рис. 4).
Характерной особенностью этого фазового портрета является то, что изоклины (26) и (27) совпадают (т. е. снова реализуется «негрубый», по А. А. Андронову, случай), что означает, что в системе имеется бесконечно большое количество состояний равновесия, к которым относятся все точки объединенных изоклин. Это в свою очередь означает, что фазовые траектории стягиваются к изоклинам, где и тормозятся. Таким образом, в результате конкурентного взаимодействия в конечном итоге устанавливается режим простого воспроизводства, при котором ситуация стабилизируется, значения MY1 и MY2 перестают изменяться, доходы равны расходам, чистая прибыль равна нулю, при этом каждая из подсистем занимает свою экономическую нишу, не подавляя друг друга. Это важный результат, показывающий, что в замкнутой системе в условиях конкуренции производителей возможны состояния равновесия, причем таких состояний может быть много. Однако рассмотренная ситуация (итоговое равновесие конкурирующих подсистем) возможна лишь при строгом выполнении равенства величин hi.
Если удельные издержки (себестоимость продукции) у одной из подсистем выше, чем у другой, например, h2 > h1, то фазовый портрет системы (23) – (24) существенно изменяется и приобретает следующий вид (рис. 5).
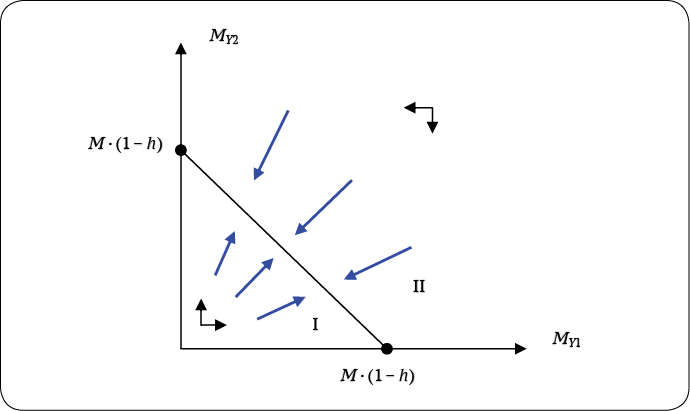
Рис. 4. Фазовый портрет системы (23) – (24) при условии hi = h
Примечание: стрелками обозначены фазовые траектории. В зоне I значения MY1 и MY2 растут, в зоне II значения MY1 и MY2 уменьшаются.
Источник: составлено автором.
Fig. 4. Phase portrait of the system (23) – (24) at hi = h
Note: the arrows denote phase trajectories. In zone I the values of MY1 and MY2 increase, in zone II the values of MY1 and MY2 decrease.
Source: сompiled by the author.

Рис. 5. Фазовый портрет системы (23) – (24) при условии h2 > h1
Примечание: жирной точкой отмечено состояние устойчивого равновесия (оно соответствует экономическому поражению второй подсистемы в конкурентной борьбе с первой подсистемой). В зоне I значения MY1 и MY2 растут, в зоне II значения MY1 и MY2 уменьшаются, в зоне III значение MY1 растет, а значение MY2 уменьшается.
Источник: составлено автором.
Fig. 5. Phase portrait of the system (23) – (24) at h2 > h1
Note: the bold point indicates a state of stable equilibrium (it corresponds to the economic defeat of the second trading corporation in competition with the first one). In zone I the values of MY1 and MY2 increase, in zone II the values of MY1 and MY2 decrease, in zone III the value of MY1 increases, and the value of MY2 decreases.
Source: сompiled by the author.
Видно, что при условии h2 ≠ h1 изоклины перестают совпадать (но по-прежнему реализуется «негрубый», по А. А. Андронову, случай) и на фазовом портрете возникает зона III, где значение MY1 растет, а значение MY2 уменьшается. При этом возможность устойчивого сосуществования двух подсистем исчезает, и подсистема с более высокими издержками в конечном итоге терпит экономическое поражение: конкуренция приводит к монополизму первой подсистемы.
Аналогичная ситуация возникает, если первая подсистема начнет производить продукцию, более привлекательную для потребителей, и потребительский спрос смещается в ее сторону. Если дополнительный спрос на продукцию первой подсистемы составляет величину δ, тогда система уравнений (14) – (20) преобразуется к виду:
dMY1 / dt = (k1 · MH1 + k2 · MH2) · (F1 · (1 + δ) / (F1 + F2)) – p · h1 · F1. (28)
dMH1/dt = p · h1 · F1 – k1 · MH1. (29)
dMY2 / dt = (k1 · MH1 + k2 · MH2) · (F2 / (F1 + F2) – F1 · δ / (F1 + F2)) – p · h2 · F2. (30)
dMH2 / dt = p · h2 · F2 – k2 · MH2. (31)
dp / dt = a · p · (k1 · MH1 / p + k2 · MH2 / p – (F1 + F2 – kY1 · MY1 / p – kY2 · MY2 / p)). (32)
Fi = fi · (kYi · MYi / p)ci. (33)
MH1 + MH2 + MY1 + MY2 = M. (34)
В уравнении (30) учтено, что увеличение спроса на продукцию первой подсистемы в силу замкнутости экономической системы автоматически приводит к снижению платежеспособного спроса на продукцию второй подсистемы.
Можно легко показать, что фазовый портрет системы (28) – (34) аналогичен портрету, изображенному на рис. 5; соответственно, даже незначительное преимущество продукции первой подсистемы над продукцией второй подсистемы в конечном итоге приводит к банкротству последней7.
Таким образом, ситуация конкурентного взаимодействия, характеризуемая рассматриваемыми уравнениями, принципиально неустойчива и при выполнении условия (25) (т. е. при «игре с нулевой суммой») неизбежно приводит к монополизму по причине наличия положительных обратных связей, в результате чего тот, кто по тем или иным причинам достиг преимущества в конкурентной борьбе, получает в дальнейшем еще больше возможностей для усиления своих позиций8.
Однако если перейти от «игры с нулевой суммой» к «игре с положительной суммой», т. е. к ситуации, когда общий ресурс в системе непрерывно растет (в нашем случае это означает рост M (t) в результате постоянной эмиссионной подкачки денег в экономическую систему9), то возникновения монополизма можно избежать. В этом случае функционирование экономической системы в режиме конкуренции может продолжаться неограниченно долго. На языке фазовых портретов это можно объяснить следующим образом.
Рассмотрим ситуацию, отображенную на рис. 5, где предполагается, что h2 > h1. Будем считать, что исходное состояние находится в зоне I, в которой наблюдается рост как MY1, так и MY2. Если бы выполнялось условие «игры с нулевой суммой» (25), то траектория системы достигла бы изоклины (27) и развернулась в направлении аттрактора, обозначенного жирной точкой, что означает подавление второй подсистемы первой подсистемой. Однако в условиях «игры с положительной суммой», когда величина M (t) постоянно увеличивается, изоклина (27) непрерывно удаляется от начала координат, расширяя зону I. Соответственно, несмотря на рост MY1 и MY2, фазовая траектория не покидает зону I и не переходит в зону III, в которой первая подсистема фатально подавляет вторую и в конечном итоге становится монополистом.
Расширение зоны I дает шанс второй подсистеме, переломить ситуацию и постараться вырваться вперед. Для этого ей нужны дополнительные финансовые средства, которые она смогла бы направить на получение преимуществ в конкурентной борьбе с первой подсистемой. Дополнительные финансовые средства обеспечивает банковский кредит, а получение преимуществ возможно за счет разработки и внедрения инноваций, повышающих производительность труда и/или улучшающих качество и привлекательность производимых товаров. Если это удается, то уже вторая подсистема вырывается вперед, а первая вынуждена догонять. И так далее (рис. 6). Аналогом такой ситуации является «бег Красной королевы» в сказке Л. Кэрролла «Приключения Алисы в Стране чудес»: приходится бежать со всех ног, чтобы только остаться на том же месте.
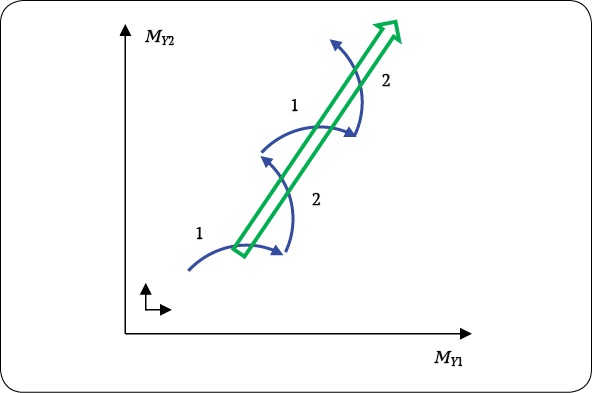
Рис. 6. Фазовая траектория в случае, когда то первая, то вторая подсистема поочередно вырываются вперед вследствие периодического внедрения технологических инноваций для получения преимущества в конкурентной борьбе
Примечание: (1) – участки фазовой траектории, когда первая подсистема получает технологическое преимущество;
(2) – участки траектории, когда вторая подсистема получает технологическое преимущество. Жирной стрелкой обозначен общий рост экономической системы.
Источник: составлено автором.
Fig. 6. Phase trajectory in the case when the first and the second subsystem alternately break ahead due
to the periodic introduction of technological innovations to gain a competitive advantage
Note: (1) – sections of the phase trajectory when the first subsystem gains a technological advantage; (2) – sections of the trajectory when the second subsystem gains a technological advantage. The bold arrow indicates the overall growth of the economic system.
Source: сompiled by the author.
Таким образом, выкладки [13. С. 45–49] приводят к заключению, что необходимым условием того, чтобы конкурентная борьба не приводила к монополизму, является непрерывный рост системы, постоянное создание условий для «игры с положительной суммой». Именно поэтому в либерально-рыночных экономиках так озабочены тем, чтобы сохранялись высокие темпы роста. Экономический рост в конкурентных рыночных системах – это не столько стремление к обеспечению материального благосостояния граждан (как это часто заявляется в пропагандистских целях), сколько стремление обеспечить устойчивость функционирования конкурентной экономики. С другой стороны, наличие конкуренции и угроза банкротства заставляют экономических агентов прилагать максимум усилий, чтобы сохранить свой бизнес, стимулируют экономическую активность, заставляют внедрять инновации, что в свою очередь создает условия для продолжения общего экономического роста10. Соответственно, система становится самосогласованной: «игра с положительной суммой» поддерживает устойчивость конкурентных взаимодействий, а конкуренция в свою очередь стимулирует активность, экономический рост, создавая условия для «игры с положительной суммой».
Приведенные выше результаты из работы [13] подтверждаются более детальными исследованиями, проводимыми на протяжении 10 лет в Институте экономики РАН под руководством академика В. И. Маевского с использованием мезоэкономических математических моделей [14–29].
Необходимость обеспечения «игры с положительной суммой» резко повышает роль финансовой системы в индустриальном обществе, поскольку с ее помощью осуществляется рост денежной массы, необходимой для расширения масштабов производства [21][25][26][28][29]. При этом в индустриальном обществе, основанном на конкуренции и частной собственности, финансовая система использует свое привилегированное положение для усиления своей экономической и, как следствие, политической власти. Основным инструментом обретения экономической власти является предоставление денежных кредитов при условии возврата денег с процентами (ростовщичество). Формально считается, что кредитный процент – это компенсация рисков невозврата выданных кредитов отдельными заемщиками, однако на практике процент перекрывает эти риски и является источником прибыли банковской системы (причем немалым). В условиях конкуренции и необходимости расширения производства производители вынуждены брать кредиты, тем самым попадая в зависимость от финансового сектора. В социалистической версии индустриального общества (СССР) финансовая система не обладала самостоятельностью и подчинялась политическим властям.
При этом важно понимать, что одной денежной эмиссии для обеспечения экономического роста недостаточно, необходимым условием реального роста является расширение ресурсной базы11 (в противном случае денежные вливания приводят лишь к инфляции12). При отсутствии роста ресурсной базы конкуренция неизбежно приводит к монополизму или к полному отказу от свободного рынка и переходу к распределительной системе с жестким регулированием (примером этого является концепт будущего общества, пропагандируемый К. Швабом [30] и сторонниками «инклюзивного капитализма»).
- Таким образом, модель (14) – (20) показывает, что условием того, что конкуренция в рыночных условиях не будет приводить к монополизму, является наличие «игры с положительной суммой». Возникает вопрос: как это соотносится с ситуациями, отображенными на рис. 2? Действительно, формально в базовой модели (3) – (4) наличие конкуренции означает отрицательность коэффициентов cijи отображается фазовыми портретами, на которых экономический рост отсутствует (рис. 2В и 2Г), так как формально отрицательность cij приводит к уменьшениюui. Это справедливо при условии, что коэффициенты ai и bi при наличии конкуренции не изменяют своих значений. Однако часто бывает так, что наличие конкуренции приводит к повышению активности акторов, опасающихся действий конкурентов. В модели (3) – (4) повышение активности можно отразить увеличением коэффициентов a1 и a2, например, следующим образом:
a1 → a1 + g1 · u2,
a2 → a2 + g2 · u1. (35)
Смысл такой записи следующий: противодействуя возникшим угрозам, i-й актор активизирует свою деятельность пропорционально уровню опасности, который в свою очередь пропорционален «силе» конкурента uj. Реальное увеличение ai зависит от имеющихся ресурсных, технических, организационных, интеллектуальных и других возможностей i-го актора, что отражает величина коэффициента gi в выражении (35).
В результате система уравнений (3) – (4) может быть переписана в виде:
du1 / dt = (a1 + g1 · u2) · u1 – b1 · u12 + c12 · u1 · u2 = a1 · u1 – b1 · u12 + (g1 + c12) · u1 · u2, (36)
du2 / dt = (a2 + g2 · u1) · u2 – b2 · u22 + c21 · u1 · u2 = a2 · u2 – b2 · u22 + (g2 + c21) · u1 · u2. (37)
Если, несмотря на cij < 0, выполняется условие (gi + cij) > 0 (т. е. если реакция на угрозу по своей эффективности превышает реальный ущерб от действий конкурента), то фазовые портреты, соответствующие уравнениям (36) – (37), в случае (g1 + c12) · (g2 + c21) > b1 · b2 приобретают вид, изображенный на рис. 2А, а в случае (g1 + c12) · (g2 + c21) < b1 · b2 – вид, изображенный на рис. 2Б. При этом ситуация, изображенная на рис. 2А, – это «игра с положительной суммой», когда конкуренция приводит не к стагнации, а к непрерывному экономическому росту13.
Таким образом, базовая модель позволяет понять, при каких условиях экономическая конкуренция способствует экономическому росту, а при каких – приводит к монополизму и экономической стагнации. Во второй части данной статьи базовая модель будет использована для анализа особенностей конкуренции в политической сфере и влияния конкуренции на социально-политические процессы (включая геополитическую динамику).
1 Применительно к биологическим системам модель конкурентного взаимодействия (2) исследовалась, например, в работах [4][5], применительно к социальным системам – в работах [6–8].
2 Для нас наиболее интересными являются случаи, когда акторы потенциально достаточно близки по «силе», поскольку в противном случае (если какой-то из акторов имеет явное преимущество в своих возможностях) результат конкурентного взаимодействия предсказуем и тривиален: более сильный актор в конечном итоге подавляет всех остальных вне зависимости от начального состояния системы.
3 Выражения для изоклин получаются, если правые части уравнений (10) и (11) приравнять нулю.
4 Данная схема является весьма упрощенной, но она не влияет на качественные выводы и принята нами для упрощения изложения.
5 Все пояснения и математические выкладки даются без купюр и берутся в качестве базовых, не требующих переформулирования, так как переформулирование может привести к утрате изначального смысла.
6 Условие замкнутости является принципиальным. Оно означает, что все товарные и денежные потоки локализованы внутри рассматриваемой экономической системы, т. е. выполняется условие автономности системы.
7 Аналогичным образом складывается ситуация, если первая подсистема стремится добиться преимущества за счет ценового демпинга.
8 В реальных ситуациях для недопущения монополизма принимаются антимонопольные законы, специальные нормативные акты, но это уже осуществление мер внешнего регулирования. Нас же интересует динамика конкурентных взаимодействий в их «чистом» виде.
9 Это может быть кредитная эмиссия предприятиям и/или населению, или увеличение денежной массы за счет увеличения государственных расходов или за счет положительного сальдо международной торговли и т. п.
10 По существу, по отношению к конкурентной рыночной экономике речь может идти только о динамическом равновесии, подобном равновесию едущего велосипедиста, которому, чтобы не упасть, надо изо всех сил крутить педали.
11 Западные страны начиная с XVIII в. поддерживали рост ресурсной базы и «игру с положительной суммой» для своих экономик, в частности, за счет политики колониализма и неоколониализма.
12 Рост может тормозиться также за счет увеличения издержек, например, на решение нарастающих экологических проблем.
13 Единственно, это осуществимо только в том случае, когда для этого есть реальные ресурсные возможности.
Список литературы
1. Плотинский Ю. М. Модели социальных процессов. Москва: Логос, 2001. 296 с.
2. Puu T. Nonlinear economic dynamics. Berlin, Heidelberg: Springer-Vergal, 1989.
3. Малков С. Ю. О методике прогнозирования предкризисного развития социально-политических систем с учетом глобальных и региональных тенденций социально-политической динамики, политических кризисов и конфликтов // Системный мониторинг глобальных и региональных рисков. Т. 11 / отв. ред. Л. Е. Гринин, А. В. Коротаев, Д. А. Быканова. Москва: Моск. ред. изд-ва «Учитель», 2020. С. 470–512.
4. Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва – Ижевск: Институт компьютерных технологий, 2003.
5. Ризниченко Г. Ю. Лекции по математическим моделям в биологии. 2-е изд., испр. и доп. Москва – Ижевск: Институт компьютерных исследований, НИЦ «Регулярная и хаотическая динамика», 2010.
6. Модель конкуренции / М. М. Зульпукаров, Д. С. Чернавский, А. В. Щербаков. Препринт ИМП РАН. № 64. Москва, 2006.
7. Малков С. Ю., Кирилюк И. Л. Моделирование динамики конкурирующих сообществ: варианты взаимодействия // Информационные войны. 2013. № 2(26). С. 49–56.
8. Малков С. Ю. Социальная самоорганизация и исторический процесс: Возможности математического моделирования. Москва: Книжный дом «Либроком», 2009.
9. Андронов А. А., Понтрягин Л. С. Грубые системы // Доклады АН СССР. 1937. Т. 14, № 5. С. 247–250.
10. Мезоэкономика: элементы новой парадигмы: монография / под ред. В. И. Маевского, С. Г. Кирдиной-Чэндлер. Москва: ИЭ РАН, 2020.
11. Новая теория воспроизводства капитала: развитие и практическое применение: монография / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн. Москва; Санкт-Петербург: Нестор-История, 2016.
12. Теория перекрывающихся поколений основного капитала / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн // Вестник Российской академии наук. 2016. Т. 86, № 1. С. 56–65.
13. Малков С. Ю. Размышления на тему: есть ли будущее у капитализма? // Информационные войны. 2021. № 4(60). С. 41–49.
14. Маевский В. И., Малков С. Ю. Переход от простого воспроизводства к экономическому росту // УФН. 2011. Т. 181, вып. 9. С. 753–757.
15. Маевский В. И., Малков С. Ю. Новый взгляд на теорию воспроизводства. Москва: ИНФРА-М, 2013.
16. Маевский В. И., Малков С. Ю. Перспективы макроэкономической теории воспроизводства // Вопросы экономики. 2014. № 4. С. 137–155. https://doi.org/10.32609/0042-8736-2014-4-137-155
17. Маевский В. И., Малков С. Ю. Кругооборот капитала и переключающийся режим воспроизводства // Urbi et orbi / под общ. ред. Р. С. Гринберга, А. Я. Рубинштейна. В 3 т. Т. 1. Теоретическая экономика. Санкт-Петербург: Алетейя, 2014. С. 525–566.
18. Maevsky V., Malkov S. New Reproduction Theory for Modern Knowledge Economy: Modeling // Socio Economic and Technological Innovation: Mechanism and Institutions / eds. K. Mandal, N. Asheulova, S. Kirdina. Narosa Publishing House Pvt. Ltd., 2014. Pр. 93–112.
19. Особенности и проблемы моделирования переключающегося воспроизводства / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн // Экономика и математические методы. 2015. Т. 51, № 1. С. 26–44.
20. Теория и модель перекрывающихся поколений основного капитала / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн. Москва: Институт экономики РАН, 2015.
21. Денежные механизмы и модель переключающегося режима воспроизводства / В. И. Маевский, С. А. Андрюшин, С. Ю. Малков, А. А. Рубинштейн // Вопросы экономики. 2016. № 9. С. 129–149. https://doi.org/10.32609/0042-8736-2016-9-129-149
22. Развитие модели переключающегося режима воспроизводства и сравнение ее с DSGE-моделью / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн // Новые исследования в гетеродоксальной экономике: российский вклад: монография / отв. ред. В. И. Маевский, С. Г. Кирдина. Mосква: ИЭ РАН, 2016. С. 268–289.
23. Анализ экономической динамики США, СССР и России с помощью модели ПРВ / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн // Вопросы экономики. 2018. № 7. С. 82–95. https://doi.org/10.32609/0042-8736-2018-7-82-95
24. Об эволюции моделей переключающегося режима воспроизводства / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн // Актуальные проблемы экономики и права. 2018. Т. 12, № 4. С. 816–827. https://dx.doi.org/10.21202/1993-047X.12.2018.4.816-827
25. Критический анализ параметров денежно-кредитной политики на основе мезоэкономической модели переключающегося режима воспроизводства / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн. Москва: ИЭ РАН, 2019.
26. Анализ связи между эмиссией, инфляцией и ростом с помощью модели переключающегося режима воспроизводства / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн // Вопросы экономики. 2019. № 8. С. 45–66. https://doi.org/10.32609/0042-8736-2019-8-45-66
27. Об одном направлении развития мезоэкономической теории / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн, Е. В. Красильникова // Journal of Institutional Studies. 2019. № 11(3). С. 21–38. https://doi.org/10.17835/2076-6297.2019.11.3.021-038
28. Теория воспроизводства капитала и не-нейтральность денег / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн, Е. В. Красильникова; под ред. акад. РАН В. И. Маевского. Москва; Санкт-Петербург: Нестор-История, 2020.
29. О долговом способе монетизации российской экономики / В. И. Маевский, С. Ю. Малков, А. А. Рубинштейн // Terra economicus. 2021. Т. 19, № 4. С. 21–35. https://doi.org/10.18522/2073-6606-2021-19-4-21-35
30. Клаус Шваб, Тьерри Маллере COVID-19: Великая перезагрузка. Женева: Форум Издательство. Вып. 1.0, 2020.
Об авторе
С. Ю. МалковРоссия
Малков Сергей Юрьевич, доктор технических наук, профессор
Web of Science Researcher ID: https://www.researcherid.com/rid/L-5734-2015, eLIBRARY ID: AuthorID: 16491
г. Москва
Конфликт интересов:
Автором не заявлен.
Рецензия
Для цитирования:
Малков С.Ю. Моделирование конкурентных взаимодействий: базовые закономерности. Часть 1. Russian Journal of Economics and Law. 2023;17(1):35-50. https://doi.org/10.21202/2782-2923.2023.1.35-50. EDN: LUERWY
For citation:
Malkov S.Yu. Modeling of competitive interactions: basic regularities. Part 1. Russian Journal of Economics and Law. 2023;17(1):35-50. (In Russ.) https://doi.org/10.21202/2782-2923.2023.1.35-50. EDN: LUERWY



































